Permasalahan-permasalahan tersebut secara ringkas bisa dilihat dalam skema berikut.
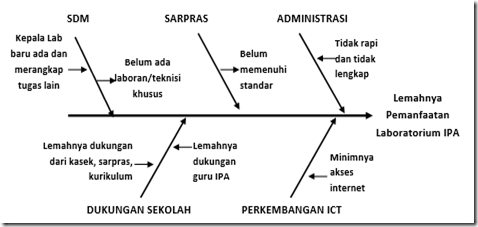
Sekarang mari kita bahas satu persatu ke-5 faktor di atas, yaitu :
1. Sumber Daya Manusia
Sumber daya manusia yang dimaksud adalah sumber daya pengelola laboratorium, yang terdiri dari kepala laboratorium, teknisi, dan laboran. Tugas dan wewenang ketiganya mengacu pada Peraturan Menteri Pendidikan Nasional RI Nomor 24 Tahun 2007, Peraturan Menteri Pendidikan Nasional RI Nomor 26 Tahun 2008, Peraturan Menteri Pendidikan Nasional RI Nomor 35 Tahun 2010 Tentang Petunjuk Teknis Pelaksanaan Jabatan Fungsional Guru dan Angka Kreditnya dan .Pedoman PK Guru dengan Tugas Tambahan Kepala Laboratorium/Bengkel Sekolah/Madrasah.
Di lapangan, banyak terjadi kepala laboratorium masih melakukan banyak tugas lain. Padahal untuk kepala laboratorium sendiri sudah dihargai 12 jam. Berdasarkan pengalaman, kalau dihitung 12 jam tersebut tidaklah cukup. Apalagi untuk menyiapkan perangkat-perangkat laboratorium yang sebelumnya belum ada.
Demikian juga, jika tenaga laboran atau teknisi sekedar diambilkan dari staff TU, misalnya. Seringnya akan terjadi bentrok tugas di antara sebagai laboran atau teknisi dengan sebagai staff TU.
2. Keterbatasan sarana dan prasarana
Adanya bantuan berupa gedung laboratorium maupun peralatannya bukan berarti tidak ada masalah yang timbul. Misalnya, jika kondisi gedungnya jauh dari pusat sekolah akan rawan pencurian.
Demikian juga bantuan alat dan bahan yang yang biasanya terbatas jumlahnya harus dicari pemecahannya.
3. Lemahnya Administrasi
Masalah administrasi terkait langsung dengan ketersediaan tenaga administrasi di laboratorium, khususnya kepala laboratorium. Dengan pengangkatan kepala laboratorium yang dihargai setara dengan 12 jam mengajar, diharapkan administrasi laboratorium dapat disusun dengan rapi dan lengkap. Tetapi sayangnya, referensi mengenai perangkat laboratorium yang sesuai tuntutan PK Guru dengan tugas tambahan kepala laboratorium sangatlah terbatas. Yang banyak ditemukan, ya perangkat standarnya saja.
4. Lemahnya dukungan sekolah
Seringkali laboratorium dijadikan alternatif ruang pertemuan bagi sekolah. Ketimbang membongkar pembatas kelas atau menggunakan sebuah kelas, lebih mudah menggunakan ruang laboratorium yang relatif luas. Demikian juga, ketika laboratorium, masih dianggap sebelah mata oleh sekolah, maka alokasi dana yang ke arah pengembangan laboratorium sangat terbatas bahkan mungkin tidak ada.
5. Perkembangan ICT
Perkembangan ICT sangat pesat. Hal ini bisa ditandai dengan merebaknya konten-konten multimedia yang begitu menarik, baik melalui internet, iklan, surat kabar, majalah, bahkan iklan-iklan di pinggir jalan.
Dengan begitu banyaknya konten seperti itu, perlu dipertanyakan kembali apakah sumber belajar (buku, lks) masih relevan pada saat sekarang. Dipungkiri atau tidak, sebagai guru atau pemerhati pendidikan seharusnya bukan sekedar melarang siswanya mengakses konten-konten “sampah”, terutama melalui internet. Tetapi, mari bersama-sama membuat konten-konten “tandingan” yang akan membuat siswa lebih tertarik pada konten yang kita buat. Konten tersebut bisa dalam bentuk presentasi pembelajaran, multimedia pembelajaran, e-book interaktif, game edukasi dan lain-lain.
Kembali ke fungsi laboratorium sebagai pusat pembelajaran IPA khususnya, perlu dipertimbangkan kembali untuk mewujudkan laboratorium yang berbasis teknologi informasi. Selain untuk menghadapi tantangan dari perkembangan teknologi informasi dan komunikasi, juga banyaknya sumber-sumber daya di internet yang dapat digunakan untuk kepentingan pendidikan maupun riset.
Bagaimana solusinya? Tunggu postingan berikutnya.
Luar biasa mata ini. Waktu menunjukkan jam 03.08 dini hari.
Sumber : Laporan OJL Penulis Arsyad Riyadi Januari 21, 2015 New Google SEO Bandung, Indonesia
Apa yang harus didapatkan oleh peserta didik, bukan hanya mencapai kompetensi pengetahuan semata, tetapi juga ketrampilan dan sikap. Untuk mencapai ketiga kompetensi tersebut, laboratorium menjadi alternatif yang sangat baik.
Di masa mendatang laboratorim impian saya, adalah bisa menjadi laoratorium yang mampu memberikan berbagai pelayanan, yaitu :
1. Kegiatan praktikum bagi seluruh siswa
2. Kegiatan penelitian bagi siswa
3. Kegiatan penelitian di luar siswa (alumni, siswa sma, mahasiswa, umum)
4. Melayani riset berbasis lab, perpustakaan, maupun internet
Berikut adalah rencana/roadmad yang telah dibuat :
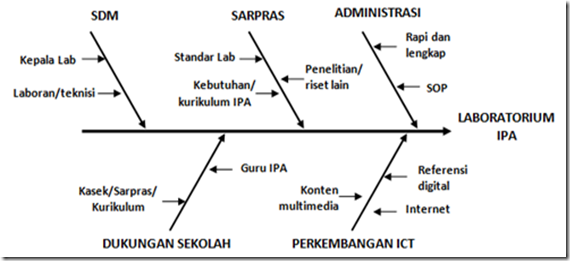 |
| Road Map Pengembangan Laboratorium IPA |
Sebagai gambaran awal, pada saat mendatang laboratorium IPA, memiliki sarana dan prasarana sebagai berikut:
1. Ruang AC yang dilengkapi LCD, Soundsytem dan tata cahaya yang baik
2. Adanya komputer/laptop/tablet yang terhubung ke internet
3. Referensi yang lengkap, terkait dengan sains, riset, perkembangan teknologi dalam buku cetak maupun dalam bentuk digital (animasi, simulasi, video, game edukasi dan lain-lain)
4. Majalah dinding (mading) baik dalam model klasik maupun digital.
5. Pengembangan Blog/Website/Portal Berbasis Sains
Terakhir, terkait dengan tuntutan perkembangan teknologi informasi dan komunikasi, laboratorium IPA juga mampu menyediakan sumber-sumber bahan ajar dalam bentuk digital :
Sumber : Laporan OJL Penulis Arsyad Riyadi Januari 21, 2015 New Google SEO Bandung, Indonesia
A. Nama Percobaan : Gaya Gerak Listrik Induksi
B.Tujuan Percobaan : Menyelidiki gejala kelistrikan yang ditimbulkan oleh induksi magnetik
C. Alat dan Bahan
| No | Nama Alat | Jml | No | Nama Alat | Jml | |
| 1. | Kabel penghubung merah | 1 | 6. | Besi inti I | 1 | |
| 2. | Kabel penghubung hitam | 1 | 7. | Penghubung jembatan | 2 | |
| 3. | Basicmeter 90 | 1 | 8. | Papan rangkaian | 1 | |
| 4. | Kumparan 1000 lilitan | 1 | 9. | Magnet batang alnico | 1 | |
| 5. | Kumparan 500 lilitan | 1 |
D. Langkah Percobaan
1. Siapkan alat dan bahan
2. Buatlah rangkaian sesuai gambar 1 :
- Saklar masih terbuka (posisi “0”)
- Basicmeter difungsikan sebagai voltmeter dengan batas ukur 100 mV DC
- Gunakan kumparan 500 lilitan


3. Periksa kembali susunan dari rangkaian
4. Dekatkan/jauhkan ujung batang magnet terhadap lubang kumparan secara perlahan-lahan . amati simpangan jarum voltmeter dan catat hasil pengukuran voltmeter ke tabel.
5. Ulangi langkah (4), tetapi dengan gerakan magnet yang lebih cepat
6. Ganti kumparan 500 lilitan dengan kumparan 1000 lilitan
7. Ulangi langkah (4) dan 5
8. Pasang (masukkan) besi inti I ke dalam kumparan 500 lilitan
9. Ulangi langkah (4) dan (5)
10. Kemasi alat dan bahan yang digunakan
E. Tabel dari Hasil Pengamatan

Sumber Materi Praktikum :
Panduan Contoh Percobaan Listrik dan Magnet, Wardhana. Arsyad Riyadi Januari 21, 2015 New Google SEO Bandung, Indonesia
Dalam kegiatan kali ini, para siswa akan melaksanakan praktikum/percobaan listrik statis. Bagaimana membuat benda menjadi bermuatan, dan bagaimana interaksi antara benda bermuatan.
Berikut adalah contoh videonya, meski agak bergoyang
Dan berikut inilah lembar kerja dari Praktikum Mengenai Gejala Listrik Statis pada Benda.
A. Tujuan Percobaan
Menyelidiki gejala listrik statis pada benda
B. Alat dan Bahan
1. Plastik/mika
2. Potongan kertas
C. Langkah Kerja
1. Dekatkan plastik/mika pada potongan kertas. Amati apa yang terjadi.
2. Dekatkan plastik/mika pada plastik/mika yang lain. Amati apa yang terjadi.
3. Dekatkan plastik/mika pada tembok. Amati apa yang terjadi.
4. Gosokkan plastik/mika pada rambut yang kering.
5. Ulangi langkah 1 – 3. Amati apa yang terjadi. (Catatan : dalam mengulangi langkah 2, kedua plastik/mika digosok)
6. Catat hasil pengamatan pada tabel berikut.
| Percobaan | Sebelum digosok | Setelah digosok |
| Didekatkan pada potongan kertas | ||
| Didekatkan pada plastik/mika lain | ||
| Didekatkan pada tembok |
D. Pertanyaan
1. Apakah ada perbedaan antara plastik/mika yang belum digosok dengan setelah digosok dengan rambut kering?
2. Apa yang terjadi ketika plastik/mika yang sudah digosok didekatkan pada potongan kertas kecil. Jelaskan!
3. Apa yang terjadi ketika plastik/mika yang sudah digosok didekatkan pada plastik/mika lain yang juga digosok. Jelaskan!
4. Apa yang terjadi ketika plastik/mika yang sudah digosok didekatkan pada tembok. Jelaskan!
E. Kesimpulan
Berdasarkan percobaan yang telah dilakukan. Bagaimana kesimpulan yang bisa diambil? Arsyad Riyadi Januari 21, 2015 New Google SEO Bandung, Indonesia
Persamaan Gerak : Kecepatan
Kecepatan, seperti diketahui, menyatakan besar perubahan posisi benda terhadap waktu.
Kecepatan rata-rata
Kecepatan rata-rata didefinisikan sebagai hasil bagi perpindahan dengan selang waktu.
dengan :
Kecepatan Sesaat
Kecepatan sesaat adalah kecepatan rata-rata untuk selang waktu mendekati nol.
v = vx i + vy j
Kecepatan sesaat sebagai kemiringan grafik perpindahan waktu
v= tan a
Besar komponen kecepatan pada sumbu x dan sumbu y adalah
Vx = v cos θ dan Vy = v sin θ
Menentukan Posisi dari Fungsi Kecepatan
dengan :
x0, y0 = koordinat posisi awal titik materi (m)
vx, vy = komponen-komponen kecepatan pada sumbu x dan y (m/s)
x, y = koordinat vektor posisi r pada saat t (m)
t = waktu (s)
Sebagai bentuk penjumlahan yang kontinu, maka posisi dapat ditentukan dengan metode grafik, yaitu :
Perpindahan = luas daerah di bawah kurva kecepatan-waktu
Contoh :
1. Posisi suatu partikel ditentukan oleh persamaan r = 3t – 5t2 dengan r dalam meter dan t dalam sekon.
Tentukan :
a) Kecepatan awal partikel
b) Kecepatan partikel pada saat t = 4 s
Penyelesaian :
a) Kecepatan awal (t = 0)
v(0) = 3 – 6.0 = 3 m/s
b) t = 4 s
v(t) = 3 – 6.4 = - 21 m/s
Untuk contoh soal yang lain, tunggulah postingan selanjutnya.
Dan untuk lebih detilnya, bisa membaca buku Terpadu Fisika SMU Kelas 3 yang ditulis oleh Bob Foster.
Arsyad Riyadi Januari 19, 2015 New Google SEO Bandung, IndonesiaVektor Posisi
Sebelum belajar lebih jauh mengenai persamaan gerakan, kita belajar dulu dasar-dasarnya yaitu mengenai vektor satuan dan vektor posisi.Vektor Satuan
Vektor satuan merupakan suatu vektor yang panjang maupun besarnya bernilai 1. Dalam suatu ruang dengan koordinat x, y, z digunakan vektor i, j, k yang mempunyai panjang atau besar satu. Vektor i, j, dan k ini berturut-turut menunjuk ke arah sumbu x, y, z.
Dalam 2 dimensi atau bidang , vektor A dapat dituliskan sebagai :
A = Ax i + Ay j
Sedangkan dalam 3 dimensi atau ruang, vektor A dapat dituliskan dalam bentuk :
A = Ax i + Ay j + Az k
Perhatikan komponen Ax, Ay, dan Az dalam bentuk skalar.
Lebih jelasnya perhatikan gambar berikut.

Vektor Posisi
Vektor posisi ini menyatakan posisi suatu titik pada suatu bidang atau ruang.
Perhatikan gambar berikut.

r(t) = vektor posisi
Δr = r2 – r1
dengan :
Δr = perpindahan posisi dari titik 1 ke titik 2
r2 = vektor posisi di titik 2
r1 = vektor posisi di titik 1
Untuk suatu titik A yang terletak dalam ruang dengan koordinat (x, y, z), vektor posisi A terhadap pusat koordinat O didefinisikan sebagai :
dengan besar vektor r adalah
Contoh :
Sebuah titik materi bergerak dari A (1,1 ,2) ke titik B (5,3,4) dalam ruang xyz. Tuliskan vektor perpindahan titik materi itu dari A ke B dan tentukan besar vektor perpindahannya!
Penyelesaian :
Vektor posisi A, rA dan vektor B, rB adalah
rA = i + j + 2k
rB = 5i + 3j + 4k
Vektor perpindahan dari A ke B adalah Δr yang didapatkan dari :
Besar vektor Δr adalah
 Arsyad Riyadi
Januari 19, 2015
New Google SEO
Bandung, Indonesia
Arsyad Riyadi
Januari 19, 2015
New Google SEO
Bandung, IndonesiaPercobaan Pompa Air
Percobaan pompa air ini merupakan salah satu materi dalam ujian praktikum fisika di sekolah yang saya ampu. Percobaan ini didasarkan pada panduan contoh percobaan mengenai hidrostatistika dan panas seperti yang diterbitkan oleh Wardhana.Tujuan Percobaan : Menyelidiki cara kerja pompa air
Alat dan Bahan
| No | Nama Alat | Jml | No | Nama Alat | Jml | |
| 1. | Dasar statif | 2 | 9. | Sumbat karet kecil 1 lubang | 1 | |
| 2. | Batang statif pendek | 1 | 10 | Sumbat karet kecil tanpa lubang | 1 | |
| 3. | Batang statif panjang | 2 | 11. | Gelas 3 arah | 2 | |
| 4. | Klem universal | 2 | 12. | Bola gelas | 2 | |
| 5. | Klem bosshead | 2 | 13. | Siring 50 ml | 1 | |
| 6. | Selang plastik | 2 | 14. | Bak plastik | 1 | |
| 7. | Selang silikon | 1 | 15. | Labu erlenmeyer | 1 | |
| 8. | Gelas beaker | 1 | 16. | Air bersih (disiapkan) | Cukup |
1. Siapkan alat dan bahan
2. Rangkaian dasar statif, batang statif pendek dan panjang, klem bosshead dan universal serta siring 50 mL sesuai gambar 1.
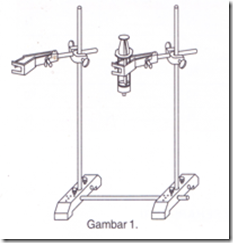
3. Jepitkan gelas tiga arah pada klem universal dan hubungkan rapat-rapat sumbat karet 1 lubang pada ujung siring sehingga terbentuk seperti gambar 2.

4. Letakkan bak plastik dalam keadaan terbalik (tengkurap). Letakkan gelas beaker di samping bak plastik dan labu erlenmeyer di atas bak plastik. Tuangkan air ±200 mL ke dalam beaker dan atur (bila perlu geser klem bosshead ke atas/bawah) agar posisi ujung kedua selang plastik menjadi sesuai gambar 3.

5. Tarik penghisap siring arah ke atas dan tekan kembali arah ke bawah. Lakukan sebanyak 3 atau 4 sambil mengamati keadaan kelereng [1] dan [2] serta arah aliran air dalam selang [a] dan [b]. Catat hasil pengamatan ke dalam tabel.
6. Tarik penghisap arah ke atas dan amati arah gerak air di sepanjang selang [a]. Amati keadaan kelereng [1] dan [2].
7. Tekan pengisap arah ke bawah dan amati arah gerak air di sepanjang selang [a] dan selang [b]. Amati pula keadaan kelereng [1] dan [2].
Tabel Hasil Pengamatan
| Penghisap siring | Bola kelereng [1] | Bola kelereng [2] | Air dalam pipa [a] | Air dalam pipa [b] |
| Diam | ||||
| Ke atas (ditarik) | ||||
| Ke bawah (ditekan) |
GERAK JATUH BEBAS
Gerak jatuh bebas adalah gerak benda yang jatuh dari ketinggian tertentu tanpa kecepatan awal.Jika hambatan udara diabaikan, maka benda-benda yang dijatuhkan dari suatu ketinggian akan mengalami percepatan yang sama. Percepatan yang dialami benda ini tidak tergantung pada bentuk, ukuran, massa, maupun komposi benda tersebut.
Aristoteles, dulu berpendapat bahwa jika ada dua benda yang berbeda massanya dijatuhkan dari ketinggian yang sama dapat dipastikan bahwa benda yang lebih berat akan sampai ke tanah terlebih dahulu. Dengan kata lain, bahwa berat benda akan berpengaruh terhadap percepatan. Semakin berat benda maka percepatannya pun semakin besar.
Pendapat Aristoteles ini, kemudian dipatahkan oleh Galileo Galileo yang menyatakan bahwa benda yang jatuh ke bawah akan mengalami percepatan yang besar. Sehingga jika ada 2 benda yang berbeda massanya dijatuhkan dari ketinggian yang sama, akan tiba ke tanah pada waktu yang bersamaan.
Perhatikan animasi berikut ini.
Persamaan yang digunakan untuk gerak jatuh bebas, sebenarnya sama dengan gerak lurus berubah beraturan (GLBB) dipercepat, dengan mengganti jarak s menjadi ketinggian y dan percepatan a menjadi percepatan gravitasi g.
v = v0 + a t menjadi v = v0 + g t
s = v0 t + ½ a t2 menjadi y = v0 t + ½ g t2
v=v02 + 2 a s menjadi v=v02 + 2 g y
Dan dengan kecepatan awal = 0, maka persamaan di atas menjadi
v = g t
y = ½ g t2
v= 2 g y
Contoh soal :
Sebuah benda dijatuhkan dari sebuah gedung setinggi 60 meter. Tentukan ketinggian benda setelah 1 s, 2s dan 4s? Diketahui percepatan gravitasi bumi 9,8 m/s2.
Penyelesaian :
Pada saat t = 1 s
y = ½ g t2 = ½ .9,8.12 = 4,9 m
Pada saat t = 2 s
y = ½ g t2 = ½ .9,8.22 = 19,6 m
Pada saat t = 4 s
y = ½ g t2 = ½ .9,8.42 = 78,4 m
Terlihat bahwa pada saat t = 4 s ternyata benda sudah sampai tanah.
Tepatnya pada detik ke- 3,5 s (dari mana ya?) Coba cek dengan menggunakan persamaan y = ½ g t2. Masukkan tinggi gedung tersebut (y) = 60 m dan g = 9,8 m/s2.
 Arsyad Riyadi
Januari 18, 2015
New Google SEO
Bandung, Indonesia
Arsyad Riyadi
Januari 18, 2015
New Google SEO
Bandung, IndonesiaSKL UN Fisika : Gerak
Indikator 2.1Menentukan besaran-besaran fisis gerak lurus, gerak melingkar beraturan, atau gerak parabola.
Materi
GERAK LURUS
Terkait dengan besaran pada gerak lurus, ada enam besaran yang tiga di antaranya merupakan besaran skalar dan tiganya lagi besaran vektor.
Besaran skalar :
Jarak dalam s
Kelajuan dalam v=Δs/Δt
Perlajuan dalam a = Δv/Δt
Besaran vektor :
Perpindahan dalam s
Kecepatan dalam v=Δs/Δt
Percepatan dalam a = Δv/Δt
Gerak Lurus Beraturan (GLB)
Pada gerak lurus beraturan, berlaku a = 0.
Grafik Gerak Lurus Beraturan (GLB)

Pada GLBB berlaku :
v = v0 + a t
s = v0 t + ½ a t2
v=v02 + 2 a s
Grafik Gerak Lurus Berubah Beraturan (GLBB)
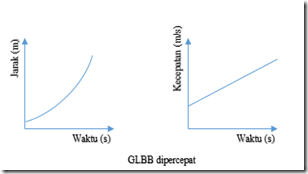

GERAK MELINGKAR BERATURAN
Gerak melingkar beraturan adalah gerak suatu benda yang lintasannya berupa lingkaran dengan kelajuan tetap. Besaran-besaran pada gerak melingkar beraturan, meliputi periode (T), frekuensi (f), kelajuan linier (v), kecepatan sudut (w), percepatan sentripetal (as) dan gaya sentripetal (F)
Periode dan frekuensi :

Kelajuan linier :

Kecepatan sudut

Hubungan antara kelajuan linier dan kecepatan sudut
v = ωr
Percepatan sentripetal :
Gaya sentripetal :
Fs = m as
GERAK PARABOLA
Gerak parabola merupakan gerak benda yang melakukan gerak lurus beraturan dan gerak lurus beraturan secara serentak. Dalam menganalisa gerak parabola ini, kita melihatnya sebagai gerak yang terpisah antara gerak lurus beraturan (GLB) pada sumbu-x dan gerak lurus berubah beraturan (GLBB) pada sumbu-y.
| Besaran | Sumbu-X | Sumbu-Y |
| Gerak lurus beraturan | Gerak lurus berubah beraturan | |
| Kecepatan awal | v0x = v0 cos α | v0y = v0 sin α |
| Perpindahan | x | y |
| Waktu | t | t |
| Percepatan | ax=0 | ay=-g |
| Kecepatan akhir | vtx = v0x | vty = v0y + ay t vty = v0y – gt |
| Perpindahan | x= v0x t | y = v0y t + ½ ay t2 y = v0y t – ½ gt2 |
Untuk soal-soalnya menyusul ya? Pada postingan berikutnya. Arsyad Riyadi Januari 18, 2015 New Google SEO Bandung, Indonesia
SKL UN Fisika : Resultan Vektor
Indikator 1.2 Menentukan resultan vektor dengan berbagai cara.1. Vektor-vektor yang saling tegak lurus
Untuk vektor-vektor yang saling tegak lurus bisa menggunakan dalil phytagoras.
Misalnya pada contoh soal berikut.
Seorang anak berjalan 50 meter ke utara, kemudian 100 m ke timur. Berapa perpindahan anak tersebut?
Penyelesaian:
Perjalanan anak tersebut dapat digambarkan dalam diagram vektor sebagai berikut.
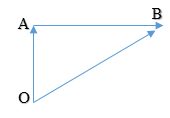
Karena yang ditanyakan perpindahan (besaran vektor), maka yang dimaksudkan adalah panjang OB (sisi miring, yang dapat dicari dengan mudah dengan menggunakan rumus phytagoras.

Hasil berbeda jika yang ditanyakan jarak atau panjang lintasan yang ditempuh (sebagai skalar), akan diperoleh : OA + OB = 50 + 100 = 150 m
2. Vektor-vektor yang tidak tegak lurus
Untuk menentukan resultan vektor tidak tegak lurus, secara grafis bisa menggunakan metode jajaran genjang atau dengan metode poligon (segi banyak).
Metode Jajaran Genjang


Metode Poligon (segi banyak)


Besar dan Arah Vektor Resultan

Arah resultan vektor R ditentukan oleh persamaan :
Contoh :
Tentukan besar dan arah dua vektor gaya sebesar 30 N dan 40 N yang membentuk sudut 600?
Penyelesaian :
Lihat gambar di atas untuk membantu penggambaran vektor dari soal ini.
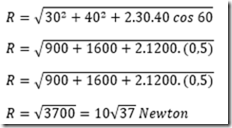
Sudut vektor resultannya diperoleh menggunakan rumus :

Komponen-komponen vektor


Dengan menggunakan penguraian vektor, kita bisa mengerjakan resultan dari vektor-vektor yang tidak saling tegak lurus, seperti pada contoh berikut

Tentukan besar dan arah resultan dari vektor-vektor tersebut di atas?
Komponen searah sumbu x

Komponen vektor searah sumbu y
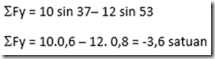
Besar resultan:
Sedangkan untuk mencari arah resultannya juga bisa menggunakan rumus :
Sehingga diperoleh :























