Paradoks AI dalam Pendidikan: Antara Efisiensi dan Jebakan Tuntutan
Administrasi Guru
-
Paradoks AI dalam Pendidikan: Antara Efisiensi dan Jebakan Tuntutan
Administrasi Guru
*Penulis:* Ariyadi | *Kategori:* Edukasi & Teknologi *Waktu Baca:...
SKL UN Fisika : Gerak
Indikator 2.1Menentukan besaran-besaran fisis gerak lurus, gerak melingkar beraturan, atau gerak parabola.
Materi
GERAK LURUS
Terkait dengan besaran pada gerak lurus, ada enam besaran yang tiga di antaranya merupakan besaran skalar dan tiganya lagi besaran vektor.
Besaran skalar :
Jarak dalam s
Kelajuan dalam v=Δs/Δt
Perlajuan dalam a = Δv/Δt
Besaran vektor :
Perpindahan dalam s
Kecepatan dalam v=Δs/Δt
Percepatan dalam a = Δv/Δt
Gerak Lurus Beraturan (GLB)
Pada gerak lurus beraturan, berlaku a = 0.
Grafik Gerak Lurus Beraturan (GLB)

Pada GLBB berlaku :
v = v0 + a t
s = v0 t + ½ a t2
v=v02 + 2 a s
Grafik Gerak Lurus Berubah Beraturan (GLBB)
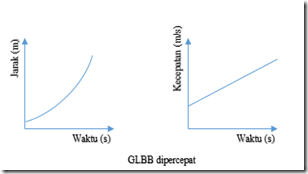

GERAK MELINGKAR BERATURAN
Gerak melingkar beraturan adalah gerak suatu benda yang lintasannya berupa lingkaran dengan kelajuan tetap. Besaran-besaran pada gerak melingkar beraturan, meliputi periode (T), frekuensi (f), kelajuan linier (v), kecepatan sudut (w), percepatan sentripetal (as) dan gaya sentripetal (F)
Periode dan frekuensi :

Kelajuan linier :

Kecepatan sudut

Hubungan antara kelajuan linier dan kecepatan sudut
v = ωr
Percepatan sentripetal :
Gaya sentripetal :
Fs = m as
GERAK PARABOLA
Gerak parabola merupakan gerak benda yang melakukan gerak lurus beraturan dan gerak lurus beraturan secara serentak. Dalam menganalisa gerak parabola ini, kita melihatnya sebagai gerak yang terpisah antara gerak lurus beraturan (GLB) pada sumbu-x dan gerak lurus berubah beraturan (GLBB) pada sumbu-y.
| Besaran | Sumbu-X | Sumbu-Y |
| Gerak lurus beraturan | Gerak lurus berubah beraturan | |
| Kecepatan awal | v0x = v0 cos α | v0y = v0 sin α |
| Perpindahan | x | y |
| Waktu | t | t |
| Percepatan | ax=0 | ay=-g |
| Kecepatan akhir | vtx = v0x | vty = v0y + ay t vty = v0y – gt |
| Perpindahan | x= v0x t | y = v0y t + ½ ay t2 y = v0y t – ½ gt2 |
Untuk soal-soalnya menyusul ya? Pada postingan berikutnya. Arsyad Riyadi Januari 18, 2015 New Google SEO Bandung, Indonesia
SKL UN Fisika : Resultan Vektor
Indikator 1.2 Menentukan resultan vektor dengan berbagai cara.1. Vektor-vektor yang saling tegak lurus
Untuk vektor-vektor yang saling tegak lurus bisa menggunakan dalil phytagoras.
Misalnya pada contoh soal berikut.
Seorang anak berjalan 50 meter ke utara, kemudian 100 m ke timur. Berapa perpindahan anak tersebut?
Penyelesaian:
Perjalanan anak tersebut dapat digambarkan dalam diagram vektor sebagai berikut.
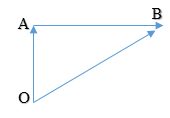
Karena yang ditanyakan perpindahan (besaran vektor), maka yang dimaksudkan adalah panjang OB (sisi miring, yang dapat dicari dengan mudah dengan menggunakan rumus phytagoras.

Hasil berbeda jika yang ditanyakan jarak atau panjang lintasan yang ditempuh (sebagai skalar), akan diperoleh : OA + OB = 50 + 100 = 150 m
2. Vektor-vektor yang tidak tegak lurus
Untuk menentukan resultan vektor tidak tegak lurus, secara grafis bisa menggunakan metode jajaran genjang atau dengan metode poligon (segi banyak).
Metode Jajaran Genjang


Metode Poligon (segi banyak)


Besar dan Arah Vektor Resultan

Arah resultan vektor R ditentukan oleh persamaan :
Contoh :
Tentukan besar dan arah dua vektor gaya sebesar 30 N dan 40 N yang membentuk sudut 600?
Penyelesaian :
Lihat gambar di atas untuk membantu penggambaran vektor dari soal ini.
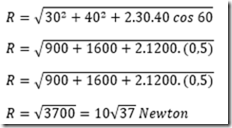
Sudut vektor resultannya diperoleh menggunakan rumus :

Komponen-komponen vektor


Dengan menggunakan penguraian vektor, kita bisa mengerjakan resultan dari vektor-vektor yang tidak saling tegak lurus, seperti pada contoh berikut

Tentukan besar dan arah resultan dari vektor-vektor tersebut di atas?
Komponen searah sumbu x

Komponen vektor searah sumbu y
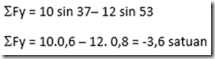
Besar resultan:
Sedangkan untuk mencari arah resultannya juga bisa menggunakan rumus :
Sehingga diperoleh :
SKL UN Fisika : Pengukuran dan Angka Penting
Indikator 1.1 Membaca hasil pengukuran suatu alat ukur dan menentukan hasil pengukuran dengan memperhatikan aturan angka penting.Pengukuran
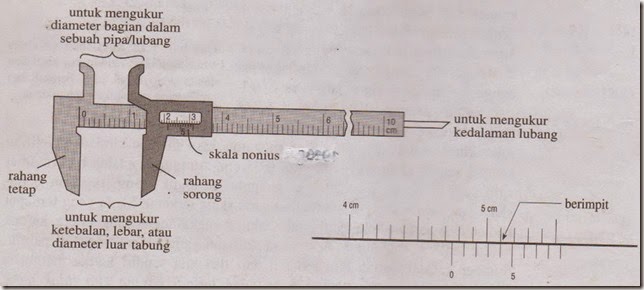
1. Menggunakan Jangka Sorong
Jangka sorong memiliki ketelian 0,1 mm atau 0,001 cm.
Bagian penting jangka sorong :
- rahang tetap
- rahang geser
 |
| Sumber : Buku Terpadu Fisika SMA Kelas X karya Bob Foster |
- Angka nol pada skala nonius berada di antara 4,7 cm dan 4,8 cm
- Garis nonius yang berhimpit dengan skala utama adalah garis ke-4
- Pembacaan jangka sorong tersebut adalah 4,7 cm + 0,04 cm = 4,74 cm
(Bagaimana? Mudah bukan?)
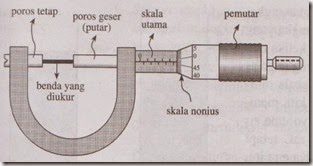
2. Mikrometer sekrup
Mikrometer sekrup ini memiliki ketelitian sampai 0,01 mm. Bagian-bagian dari mikrometer sekrup ini meliputi rahang tetap, rahang geser, kunci, skala tetap, skala putar dan pemutar (teromol).
 |
| Sumber : Buku Terpadu Fisika SMA Kelas X karya Bob Foster |
 |
| Sumber : Buku Terpadu Fisika SMA Kelas X karya Bob Foster |
Skala putar menunjukkan : 7 x 0,01 mm = 0,07 mm
Sehingga hasil pengukurannya adalah 2,57 mm
Angka Penting
Untuk materi ini, secara detailnya bisa melihat di postingan tentang angka penting, dari pengertian, aturan penulisan sampai operasi penghitungannya.
Secara ringkasnya, aturan untuk penjumlahan/pengurangan dan perkalian/pembagian adalah sebagai berikut :
- Pada saat melakukan penjumlahan atau pengurangan, banyaknya angka penting yang dihitung didasarkan pada banyaknya angka di belakang koma yang paling sedikit.
Contohnya :
210, 5 (satu di belakang koma) + 10, 43 (dua di belakang koma) = 220,93 = 220,9 (satu angka di belakang koma)
- Pada saat melakukan perkalian atau pembagian, banyaknya angka penting yang dihasilkan sama dengan banyaknya akngak penting dari bilangan yang memiliki angka penting paling sedikit.
Contohnya :
2,21 (tiga angka penting) x 2,1 (dua angka penting) = 4,641 = 4,6 (dua angka penting) Arsyad Riyadi Januari 18, 2015 New Google SEO Bandung, Indonesia
Menghitung Resultan Vektor
Melanjutkan postingan kemarin yang tentang Resultan vektor yang belum ada contoh soalnya. Pada postingan kali ini, kita akan membahas resultan vektor, untuk 2 vektor yang tidak saling tegak lurus, maupun 3 atau lebih vektor.1. Dua buah vektor, masing-masing 10 dan 8 satuan yang membentuk sudut 600 satu sama lain. Tentukan resultan vektor-vektor ini?
Penyelesaian :
Sebelumnya, kita gambarkan dulu diagram vektornya untuk memperjelas permasalahan ini.
2. Perhatikan gambar berikut. Empat buah vektor gaya yang bekerja pada sebuah benda. Tentukan resultannya?

Penyelesaian.
Uraikan dulu vektor-vektor dalam Fx dan Fy, dengan : Fx = F cos α dan Fy = F sin α, seperti tabel berikut :
| F | Sudut | Fx | Fy |
| 10 N | 300 | 5,00 | 8,66 |
| 12 N | 1350 | 8,49 | -8,49 |
| 8 N | 1800 | 0,00 | -8,00 |
| 12 N | 2400 | -10,39 | -6,00 |
| Jumlah | ΣFx =3,09 | ΣFy =-13,83 |
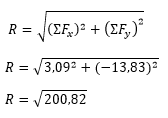
R = 14, 17 Newton
(Catatan : penghitungan soal ini menggunakan bantuan Excel) Arsyad Riyadi Januari 17, 2015 New Google SEO Bandung, Indonesia
Arsyad Riyadi Januari 17, 2015 New Google SEO Bandung, IndonesiaPenerapan Hukum Newton (1) : Soal Keseimbangan
Mengutip dari buku Terpadu Fisika SMA untuk kelas X dari Bob Foster, dalam menyelesaikan soal keseimbangan yang terkait dengan hukum II Newton, ada tahap-tahap yang perlu dilakukan :
1. Gambarlah/buatlah diagram dari sistem yang akan diselesaikan
2. Gambarkan semua gaya yang bekerja pada masing-masing benda
3. Tentukan sumbu x dan sumbu y untuk mempermudah perhitungan
4. Gambarkan diagram gaya untuk masing-masing bendanya secara terpisah
5. Berdasar diagram gaya yang dibuat, tuliskan hukum II Newton dalam komponen-komponennya :
∑Fx = max; ∑Fy = may
Kemudian, selesaikan persamaan tersebut untuk mencari besaran yang ditanyakan.
Contoh :
Sebuah pigura digantung di dinding menggunakan tali, seperti pada gambar berikut. Jika berat pigura 10N, tentukan besar tegangan masing-masing tali?
Penyelesaian :
Gambar pada soal diperbesar untuk memperjelas dalam penguraian gaya-gaya yang bekerja.
Coba perhatikan. Dalam keadaan seimbang, berlaku :
∑F = T1 + T2 + W = 0
Berdasar gambar di atas, didapatkan :
∑FX = T2 cos 600 – T1 cos 300 = 0 ……...(i)
∑Fy = T1 sin 300 + T2 sin 600 - W= 0 ……(ii)
Dari persamaan (i) didapatkan, bahwa
T2 cos 600 = T1 cos 300
Diperoleh
…………………(iii)
Dengan memasukkanke dalam persamaan (ii) didapatkan, bahwa :
T1 sin 300 + T2 sin 600 - W= 0
2T1 = 10, maka diperoleh :
T1 = 10/2 = 5 N
Masukkan T1 = 5 N ke persamaan (iii), sehingga diperoleh
Resultan Vektor
Sebelumnya mari kita ingat kembali perbedaan antara besaran vektor dan skalar. Besaran skalar dapat didefinisikan sebagai besaran yang memiliki besar atau nilai saja. Misalnya : panjang, massa, waktu, energi, suhu dan sebagainya. Sedangkan besaran vektor adalah besaran yang mempunyai besar dan arah. Misalnya perpindahan, kecepatan, percepatan, gaya, medan listrik dan medan magnet.Operasi penjumlahan maupun pengurangan pada skalar sama halnya dengan penjumlahan atau pengurangan secara aljabar. Sedangkan untuk vektor menggunakan aturan khusus, bisa menggunakan grafik maupun secara analitik.
Dalam tulisan ini, akan dibahas penjumlah vektor secara analitik.
Sebuah vektor V, dapat diuraikan menjadi komponen-komponennya, katakan namanya Vx dan Vy, sebagai berikut.

Besarnya komponen vektor Vx dan Vy dinyatakan dengan :

Besar vektor V dan sudut α dapat dituliskan sebagai

Penjumlahan vektor secara analitik
Jika R adalah jumlah dari 3 vektor V1, V2, V3, maka berlaku :
R = V1 + V2 + V3
RX = V1X + V2X + V3X
RY= V1Y + V2Y + V3Y
Besar dan arah vektor R dapat dicari dengan persamaan :

Untuk penjumlahan 2 vektor, besar vektor R dapat ditentukan dengan persamaan :

dengan θ adalah sudut apit antara V1 dan V2, sedangkan V1 dan V2 adalah besar vektor V1 dan V2.
Rumus di atas diturunkan sebagai berikut.

Dengan bantuan gambar di atas dan dari rumus cosinus kita peroleh :

Rumus ini berlaku juga ketika digunakan untuk menghitung resultan dari buah gaya, yang tidak saling tegak lurus. Penjelasan ini sekaligus menjawab pertanyaan dari beberapa teman, terkait dengan penghitungan resultan gaya untuk gaya-gaya yang tidak saling tegak lurus. Ingat…ingat…gaya termasuk besaran vektor.
Ini dulu, untuk contoh soalnya menyusul. Terlalu melelahkan posting materi yang menuntut adanya gambar dan penulisan rumus-rumus. Arsyad Riyadi Januari 16, 2015 New Google SEO Bandung, Indonesia
Kompetensi :
Mengaplikasikan konsep pertumbuhan dan perkembangan, kelangsungan hidup dan pewarisan
sifat pada organisme serta kaitannya dengan lingkungan, teknologi dan masyarakat.
Indikator :
Menjelaskan pemanfaatan bioteknologi untuk kehidupan manusia.
Materi :
Bioteknologi adalah pemanfaatan prinsip-prinsip ilmiah yang menggunakan makhluk hidup untuk menghasilkan produk dan jasa guna kepentingan manusia.
Bioteknologi Konvensional
1. Pengolahan Bahan Makanan
Bioteknologi konvensional merupakan bioteknologi yang memanfaatkan mikroorganisme untuk memproduksi alkohol, asam asetat, gula, atau bahan makanan, seperti tempe, tape, oncom, dan kecap. Ciri khas yang tampak pada bioteknologi konvensional, yaitu adanya penggunaan makhluk hidup secara langsung dan belum tahu adanya penggunaan enzim.
- Pengolahan susu menjadi yoghurt, keju, dan mentega.
Dalam pembuatan yoghurt dibutuhkan bakteri Lactobacillus bulgaricus dan Streptococcus thermophillus. Dalam pembuatan keju digunakan bakteri asam laktat, yaitu Lactobacillus dan Streptococcus. Dalam pembuatan mentega digunakan mikroorganisme Streptococcus lactis dan Lectonostoceremoris.
- Dalam pembuatan kecap, jamur, diperlukan Aspergillus oryzae.
- Dalam proses pembuatan tempe paling sedikit diperlukan empat jenis kapang dari genus Rhizopus,
yaitu Rhyzopus oligosporus, Rhyzopus stolonifer, Rhyzopus arrhizus, dan Rhyzopus oryzae.
2. Bidang Pertanian
a. Penanaman secara hidroponik
Hidroponik berasal dari kata bahasa Yunani hydro yang berarti air dan ponos yang berarti bekerja. Jadi, hidroponik artinya pengerjaan air atau bekerja dengan air.
Adapun metode yang digunakan dalam hidroponik, antara lain metode kultur air (menggunakan media air), metode kultur pasir (menggunakan media pasir), dan metode porus (menggunakan media kerikil, pecahan batu bata, dan lain-lain).
b. Penanaman secara aeroponik
Aeroponik berasal dari kata aero yang berarti udara dan ponos yang berarti daya. Jadi, aeroponik adalah pemberdayaan udara.
Bioteknologi Modern
a. Rekayasa genetika
Rekayasa genetika merupakan suatu cara memanipulasikan gen untuk menghasilkan makhluk hidup baru dengan sifat yang diinginkan. Rekayasa genetika disebut juga pencangkokan gen atau rekombinasi DNA.
Untuk mengubah DNA sel dapat dilakukan melalui banyak cara, misalnya melalui transplantasi inti, fusi sel, teknologi plasmid, dan rekombinasi DNA.
b. Bioteknologi bidang kedokteran
Misalnya dalam pembuatan antibodi monoklonal, vaksin, antibiotika dan hormon.
c. Bioteknologi bidang pertanian
1) Pembuatan tumbuhan yang mampu mengikat nitrogen
2) Pembuatan tumbuhan tahan hama
d. Bioteknologi bidang peternakan
Misalnya produksi hormon pertumbuhan yang dapat merangsang pertumbuhan hewan ternak
e. Bioteknologi bahan bakar masa depan
Misalnya gasbio (metana) dan gasahol (alkohol).
f. Bioteknologi pengolahan limbah
Salah satu contoh proses daur ulang sampah yang telah diuji pada beberapa sampah tumbuhan adalah proses pirolisis. Proses pirolisis yaitu proses dekomposisi bahan-bahan sampah dengan suhu tinggi pada kondisi tanpa oksigen. Dengan cara ini sampah dapat diubah menjadi arang, gas (misal: metana) dan bahan anorganik.
Sumber Bacaan :
Wariyono, Sukis. 2008. Mari Belajar Ilmu Alam Sekitar 3: Panduan Belajar IPA terpadu untuk Kelas IX SMP/MTs. Jakarta : Pusat Perbukuan, Departemen Pendidikan Nasional Arsyad Riyadi Januari 14, 2015 New Google SEO Bandung, Indonesia
Mengaplikasikan konsep pertumbuhan dan perkembangan, kelangsungan hidup dan pewarisan
sifat pada organisme serta kaitannya dengan lingkungan, teknologi dan masyarakat.
Indikator :
Menjelaskan pemanfaatan bioteknologi untuk kehidupan manusia.
Materi :
 |
| Tempe, produk teknologi konvensional |
Bioteknologi Konvensional
1. Pengolahan Bahan Makanan
Bioteknologi konvensional merupakan bioteknologi yang memanfaatkan mikroorganisme untuk memproduksi alkohol, asam asetat, gula, atau bahan makanan, seperti tempe, tape, oncom, dan kecap. Ciri khas yang tampak pada bioteknologi konvensional, yaitu adanya penggunaan makhluk hidup secara langsung dan belum tahu adanya penggunaan enzim.
- Pengolahan susu menjadi yoghurt, keju, dan mentega.
Dalam pembuatan yoghurt dibutuhkan bakteri Lactobacillus bulgaricus dan Streptococcus thermophillus. Dalam pembuatan keju digunakan bakteri asam laktat, yaitu Lactobacillus dan Streptococcus. Dalam pembuatan mentega digunakan mikroorganisme Streptococcus lactis dan Lectonostoceremoris.
- Dalam pembuatan kecap, jamur, diperlukan Aspergillus oryzae.
- Dalam proses pembuatan tempe paling sedikit diperlukan empat jenis kapang dari genus Rhizopus,
yaitu Rhyzopus oligosporus, Rhyzopus stolonifer, Rhyzopus arrhizus, dan Rhyzopus oryzae.
2. Bidang Pertanian
a. Penanaman secara hidroponik
Hidroponik berasal dari kata bahasa Yunani hydro yang berarti air dan ponos yang berarti bekerja. Jadi, hidroponik artinya pengerjaan air atau bekerja dengan air.
Adapun metode yang digunakan dalam hidroponik, antara lain metode kultur air (menggunakan media air), metode kultur pasir (menggunakan media pasir), dan metode porus (menggunakan media kerikil, pecahan batu bata, dan lain-lain).
b. Penanaman secara aeroponik
Aeroponik berasal dari kata aero yang berarti udara dan ponos yang berarti daya. Jadi, aeroponik adalah pemberdayaan udara.
Bioteknologi Modern
a. Rekayasa genetika
Rekayasa genetika merupakan suatu cara memanipulasikan gen untuk menghasilkan makhluk hidup baru dengan sifat yang diinginkan. Rekayasa genetika disebut juga pencangkokan gen atau rekombinasi DNA.
Untuk mengubah DNA sel dapat dilakukan melalui banyak cara, misalnya melalui transplantasi inti, fusi sel, teknologi plasmid, dan rekombinasi DNA.
b. Bioteknologi bidang kedokteran
Misalnya dalam pembuatan antibodi monoklonal, vaksin, antibiotika dan hormon.
c. Bioteknologi bidang pertanian
1) Pembuatan tumbuhan yang mampu mengikat nitrogen
2) Pembuatan tumbuhan tahan hama
d. Bioteknologi bidang peternakan
Misalnya produksi hormon pertumbuhan yang dapat merangsang pertumbuhan hewan ternak
e. Bioteknologi bahan bakar masa depan
Misalnya gasbio (metana) dan gasahol (alkohol).
f. Bioteknologi pengolahan limbah
Salah satu contoh proses daur ulang sampah yang telah diuji pada beberapa sampah tumbuhan adalah proses pirolisis. Proses pirolisis yaitu proses dekomposisi bahan-bahan sampah dengan suhu tinggi pada kondisi tanpa oksigen. Dengan cara ini sampah dapat diubah menjadi arang, gas (misal: metana) dan bahan anorganik.
Sumber Bacaan :
Wariyono, Sukis. 2008. Mari Belajar Ilmu Alam Sekitar 3: Panduan Belajar IPA terpadu untuk Kelas IX SMP/MTs. Jakarta : Pusat Perbukuan, Departemen Pendidikan Nasional Arsyad Riyadi Januari 14, 2015 New Google SEO Bandung, Indonesia
SKL UN IPA 39 : Hukum Mendel
Kompetensi :
Mengaplikasikan konsep pertumbuhan dan perkembangan, kelangsungan hidup dan pewarisan
sifat pada organisme serta kaitannya dengan lingkungan, teknologi dan masyarakat.
Indikator :
Menginterpretasi proses persilangan berdasarkan hukum Mendel.
Materi :
Pewarisan sifat dari induk kepada keturunannya disebut hereditas. Cabang biologi yang khusus mempelajari tentang hereditas adalah genetika. Tokoh yang sangat berjasa dalam menemukan hukum-hukum genetika adalah Gregor Johann Mendel (1822 – 1884) dari Austria.
 |
| Bapak Genetika, Gregor Johann Mendel |
1. Persilangan monohibrid.
Persilangan monohibrid adalah persilangan antara dua individu dengan satu sifat beda.
Persilangan dominan penuh
Persilangan antara kacang ercis berbunga merah dominan dengan kacang ercis berwarna putih resesif.
F2
| M | m | |
| M | MM (merah) | Mm (merah) |
| m | Mm (merah) | mm (putih) |
Perbandingan genotipe F2 = MM : Mm : mm = 1 : 2 : 1
Perbandingan fenotipe F2 = Merah : Putih = 3 : 1
Persilangannya dominan tidak penuh (intermediat)
Contoh :
Persilangan antara tanaman bunga pukul empat dengan sifat intermediat (dominan tidak penuh).
Dari persilangan filial (F1) diperoleh :
Perbandingan genotipe F2 = MM : Mm : mm = 1 : 2 : 1
Perbandingan fenotipe F2 = Merah : Merah muda : Putih = 1 : 2 : 1
2. Persilangan Dihibrid
Persilangan dihibrid adalah persilangan antara dua individu dengan dua sifat beda.
Contoh :
Persilangan antara kapri (ercis) biji bulat warna kuning dengan kapri biji keriput warna hijau
Dari persilangan sesama filial 1 fenotipe (F1) didapatkan:
Atas dasar gamet tersebut, terbentuknya F2 dapat disusun sebagai berikut.
| BK | Bk | bK | bk | |
| BK | BBKK (1) | BBKk (2) | BbKK (3) | BbKk (4) |
| Bk | BBKk (5) | BBkk (6) | BbKk (7) | Bbkk (8) |
| bK | BbKK (9) | BbKk (10) | bbKK (11) | bbKk (12) |
| bk | BbKk (13) | Bbkk (14) | bbKk (15) | bbkk (16) |
= BBKK : BBKk : BkKK : BbKk : BBkk : Bbkk : bbKK : bbKk : bbkk
= 1 : 2 : 2 : 4 : 1 : 2 : 1 : 2 : 1
Perbandingan fenotipe F2
= bulat kuning : bulat hijau : keriput kuning : keriput hijau
= 9 : 3 : 3 :1
Sumber Bacaan :
Wariyono, Sukis. 2008. Mari Belajar Ilmu Alam Sekitar 3: Panduan Belajar IPA terpadu untuk Kelas IX SMP/MTs. Jakarta : Pusat Perbukuan, Departemen Pendidikan Nasional Arsyad Riyadi Januari 14, 2015 New Google SEO Bandung, Indonesia

























