Vektor Posisi

Vektor Posisi

Sebelum belajar lebih jauh mengenai persamaan gerakan, kita belajar dulu dasar-dasarnya yaitu mengenai vektor satuan dan vektor posisi.
Vektor Satuan
Vektor satuan merupakan suatu vektor yang panjang maupun besarnya bernilai 1. Dalam suatu ruang dengan koordinat x, y, z digunakan vektor i, j, k yang mempunyai panjang atau besar satu. Vektor i, j, dan k ini berturut-turut menunjuk ke arah sumbu x, y, z.
Dalam 2 dimensi atau bidang , vektor A dapat dituliskan sebagai :
A = A_x i + A_y j
Sedangkan dalam 3 dimensi atau ruang, vektor A dapat dituliskan dalam bentuk :
A = A_x i + A_y j + A_z k
Perhatikan komponen A_x, A_y, dan A_z dalam bentuk skalar.
Lebih jelasnya perhatikan gambar berikut.

Vektor Posisi
Vektor posisi ini menyatakan posisi suatu titik pada suatu bidang atau ruang.
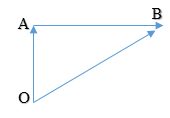
Perhatikan gambar berikut.

r(t) = vektor posisi
Δr = r₂ – r₁
dengan :
Δr = perpindahan posisi dari titik 1 ke titik 2
r₂ = vektor posisi di titik 2
r₁ = vektor posisi di titik 1
Untuk suatu titik A yang terletak dalam ruang dengan koordinat (x, y, z), vektor posisi A terhadap pusat koordinat O didefinisikan sebagai :

dengan besar vektor r adalah

Contoh :
Sebuah titik materi bergerak dari A (1,1 ,2) ke titik B (5,3,4) dalam ruang xyz. Tuliskan vektor perpindahan titik materi itu dari A ke B dan tentukan besar vektor perpindahannya!
Penyelesaian :
Vektor posisi A, r_A dan vektor B, r_B adalah
r_A = i + j + 2k
r_B = 5i + 3j + 4k
Vektor perpindahan dari A ke B adalah Δr yang didapatkan dari :

Besar vektor Δr adalah

Read More

Percobaan Fisika : Pompa Air

Percobaan Pompa Air

Percobaan pompa air ini merupakan salah satu materi dalam  ujian praktikum fisika di sekolah yang saya ampu. Percobaan ini didasarkan pada panduan contoh percobaan mengenai hidrostatistika dan panas seperti yang diterbitkan oleh Wardhana.
Tujuan Percobaan : Menyelidiki cara kerja pompa air
Alat dan Bahan

No	Nama Alat	Jml		No	Nama Alat	Jml
1.	Dasar statif	2		9.	Sumbat karet kecil 1 lubang	1
2.	Batang statif pendek	1		10	Sumbat karet kecil tanpa lubang	1
3.	Batang statif panjang	2		11.	Gelas 3 arah	2
4.	Klem universal	2		12.	Bola gelas	2
5.	Klem bosshead	2		13.	Siring 50 ml	1
6.	Selang plastik	2		14.	Bak plastik	1
7.	Selang silikon	1		15.	Labu erlenmeyer	1
8.	Gelas beaker	1		16.	Air bersih (disiapkan)	Cukup

Langkah Percobaan
1. Siapkan alat dan bahan
2. Rangkaian dasar statif, batang statif pendek dan panjang, klem bosshead dan universal serta siring 50 mL sesuai gambar 1.

3. Jepitkan gelas tiga arah pada klem universal dan hubungkan rapat-rapat sumbat karet 1 lubang pada ujung siring sehingga terbentuk seperti gambar 2.

4. Letakkan bak plastik dalam keadaan terbalik (tengkurap). Letakkan gelas beaker di samping bak plastik dan labu erlenmeyer di atas bak plastik. Tuangkan air ±200 mL ke dalam beaker dan atur (bila perlu geser klem bosshead ke atas/bawah) agar posisi ujung kedua selang plastik menjadi sesuai gambar 3.

5. Tarik penghisap siring arah ke atas dan tekan kembali arah ke bawah. Lakukan sebanyak 3 atau 4 sambil mengamati keadaan kelereng [1] dan [2] serta arah aliran air dalam selang [a] dan [b]. Catat hasil pengamatan ke dalam tabel.
6. Tarik penghisap arah ke atas dan amati arah gerak air di sepanjang selang [a]. Amati keadaan kelereng [1] dan [2].
7. Tekan pengisap arah ke bawah dan amati arah gerak air di sepanjang selang [a] dan selang [b]. Amati pula keadaan kelereng [1] dan [2].
Tabel Hasil Pengamatan

Penghisap siring	Bola kelereng [1]	Bola kelereng [2]	Air dalam pipa [a]	Air dalam pipa [b]
Diam
Ke atas (ditarik)
Ke bawah (ditekan)

Read More

GERAK JATUH BEBAS

GERAK JATUH BEBAS

Gerak jatuh bebas adalah gerak benda yang jatuh dari ketinggian tertentu tanpa kecepatan awal.
Jika hambatan udara diabaikan, maka benda-benda yang dijatuhkan dari suatu ketinggian akan mengalami percepatan yang sama. Percepatan yang dialami benda ini tidak tergantung pada bentuk, ukuran, massa, maupun komposi benda tersebut.
Aristoteles, dulu berpendapat bahwa jika ada dua benda yang berbeda massanya dijatuhkan dari ketinggian yang sama dapat dipastikan bahwa benda yang lebih berat akan sampai ke tanah terlebih dahulu. Dengan kata lain, bahwa berat benda akan berpengaruh terhadap percepatan. Semakin berat benda maka percepatannya pun semakin besar.
Pendapat Aristoteles ini, kemudian dipatahkan oleh Galileo Galileo yang menyatakan bahwa benda yang jatuh ke bawah akan mengalami percepatan yang besar. Sehingga jika ada 2 benda yang berbeda massanya dijatuhkan dari ketinggian yang sama, akan tiba ke tanah pada waktu yang bersamaan.
Perhatikan animasi berikut ini.

Persamaan yang digunakan untuk gerak jatuh bebas, sebenarnya sama dengan gerak lurus berubah beraturan (GLBB) dipercepat, dengan mengganti jarak s menjadi ketinggian y dan percepatan a menjadi percepatan gravitasi g.
v = v₀ + a t menjadi v = v₀ + g t
s = v₀ t + ½ a t² menjadi y = v₀ t + ½ g t²
v=v₀² + 2 a s menjadi v=v₀² + 2 g y
Dan dengan kecepatan awal = 0, maka persamaan di atas menjadi
v = g t
y = ½ g t²
v= 2 g y
Contoh soal :
Sebuah benda dijatuhkan dari sebuah gedung setinggi 60 meter. Tentukan ketinggian benda setelah 1 s, 2s dan 4s? Diketahui percepatan gravitasi bumi 9,8 m/s².
Penyelesaian :
Pada saat t = 1 s
y = ½ g t² = ½ .9,8.1² = 4,9 m
Pada saat t = 2 s
y = ½ g t² = ½ .9,8.2² = 19,6 m
Pada saat t = 4 s
y = ½ g t² = ½ .9,8.4² = 78,4 m
Terlihat bahwa pada saat t = 4 s ternyata benda sudah sampai tanah.
Tepatnya pada detik ke- 3,5 s (dari mana ya?) Coba cek dengan menggunakan persamaan y = ½ g t². Masukkan tinggi gedung tersebut (y) = 60 m dan g = 9,8 m/s².

Read More

SKL UN Fisika : Gerak

SKL UN Fisika : Gerak

Indikator 2.1
Menentukan besaran-besaran fisis gerak lurus, gerak melingkar beraturan, atau gerak parabola.

Materi

GERAK LURUS
Terkait dengan besaran pada gerak lurus, ada enam besaran yang tiga di antaranya merupakan besaran skalar dan tiganya lagi besaran vektor.
Besaran skalar :
Jarak dalam s
Kelajuan dalam v=Δs/Δt
Perlajuan dalam a = Δv/Δt
Besaran vektor :
Perpindahan dalam s
Kecepatan dalam v=Δs/Δt
Percepatan dalam a = Δv/Δt

Gerak Lurus Beraturan (GLB)
Pada gerak lurus beraturan, berlaku a = 0.

Grafik Gerak Lurus Beraturan (GLB)

Pada GLBB berlaku :
v = v₀ + a t
s = v₀ t + ½ a t²
v=v₀² + 2 a s
Grafik Gerak Lurus Berubah Beraturan (GLBB)




GERAK MELINGKAR BERATURAN
Gerak melingkar beraturan adalah gerak suatu benda yang lintasannya berupa lingkaran dengan kelajuan tetap. Besaran-besaran pada gerak melingkar beraturan, meliputi periode (T), frekuensi (f), kelajuan linier (v), kecepatan sudut (w), percepatan sentripetal (a_s) dan gaya sentripetal (F)
Periode dan frekuensi :

Kelajuan linier :

Kecepatan sudut

Hubungan antara kelajuan linier dan kecepatan sudut
v = ωr
Percepatan sentripetal :

Gaya sentripetal :
F_s = m a_s

GERAK PARABOLA
Gerak parabola merupakan gerak benda yang melakukan gerak lurus beraturan dan gerak lurus beraturan secara serentak. Dalam menganalisa gerak parabola ini, kita melihatnya sebagai gerak yang terpisah antara gerak lurus beraturan (GLB) pada sumbu-x dan gerak lurus berubah beraturan (GLBB) pada sumbu-y.

Besaran	Sumbu-X	Sumbu-Y
	Gerak lurus beraturan	Gerak lurus berubah beraturan
Kecepatan awal	v0x = v0 cos α	v0y = v0 sin α
Perpindahan	x	y
Waktu	t	t
Percepatan	ax=0	ay=-g
Kecepatan akhir	vtx = v0x	vty = v0y + ay t vty = v0y – gt
Perpindahan	x= v0x t	y = v0y t + ½ ay t2 y = v0y t – ½ gt2

Untuk soal-soalnya menyusul ya? Pada postingan berikutnya.

Read More

SKL UN Fisika : Resultan Vektor

SKL UN Fisika : Resultan Vektor

Indikator 1.2 Menentukan resultan vektor dengan berbagai cara.

1. Vektor-vektor yang saling tegak lurus
Untuk vektor-vektor yang saling tegak lurus bisa menggunakan dalil phytagoras.
Misalnya pada contoh soal berikut.
Seorang anak berjalan 50 meter ke utara, kemudian 100 m ke timur. Berapa perpindahan anak tersebut?
Penyelesaian:
Perjalanan anak tersebut dapat digambarkan dalam diagram vektor sebagai berikut.

Karena yang ditanyakan perpindahan (besaran vektor), maka yang dimaksudkan adalah panjang OB (sisi miring, yang dapat dicari dengan mudah dengan menggunakan rumus phytagoras.

Hasil berbeda jika yang ditanyakan jarak atau panjang lintasan yang ditempuh (sebagai skalar), akan diperoleh : OA + OB = 50 + 100 = 150 m
2. Vektor-vektor yang tidak tegak lurus
Untuk menentukan resultan vektor tidak tegak lurus, secara grafis bisa menggunakan metode jajaran genjang atau dengan metode poligon (segi banyak).
Metode Jajaran Genjang



Metode Poligon (segi banyak)


Besar dan Arah Vektor Resultan


Arah resultan vektor R ditentukan oleh persamaan :

Contoh :
Tentukan besar dan arah dua vektor gaya sebesar 30 N dan 40 N yang membentuk sudut 60⁰?
Penyelesaian :
Lihat gambar di atas untuk membantu penggambaran vektor dari soal ini.

Sudut vektor resultannya diperoleh menggunakan rumus :

Komponen-komponen vektor


Dengan menggunakan penguraian vektor, kita bisa mengerjakan resultan dari vektor-vektor yang tidak saling tegak lurus, seperti pada contoh berikut

Tentukan besar dan arah resultan dari vektor-vektor tersebut di atas?
Komponen searah sumbu x

Komponen vektor searah sumbu y

Besar resultan:

Sedangkan untuk mencari arah resultannya juga bisa menggunakan rumus :

Sehingga diperoleh :

Read More

SKL UN Fisika : Pengukuran dan Angka Penting

SKL UN Fisika  : Pengukuran dan Angka Penting

Indikator 1.1 Membaca hasil pengukuran suatu alat ukur dan menentukan hasil pengukuran dengan memperhatikan aturan angka penting.

Pengukuran
1. Menggunakan Jangka Sorong
Jangka sorong memiliki ketelian 0,1 mm atau 0,001 cm.
Bagian penting jangka sorong :
- rahang tetap
- rahang geser

Sumber : Buku Terpadu Fisika SMA Kelas X karya Bob Foster

Contoh pembacaan jangka sorong seperti pada gambar di atas adalah
- Angka nol pada skala nonius berada di antara 4,7 cm dan 4,8 cm
- Garis nonius yang berhimpit dengan skala utama adalah garis ke-4
- Pembacaan jangka sorong tersebut adalah 4,7 cm + 0,04 cm = 4,74 cm
(Bagaimana? Mudah bukan?)
2. Mikrometer sekrup
Mikrometer sekrup ini memiliki ketelitian sampai 0,01 mm. Bagian-bagian dari mikrometer sekrup ini meliputi rahang tetap, rahang geser, kunci, skala tetap, skala putar dan pemutar (teromol).

Sumber : Buku Terpadu Fisika SMA Kelas X karya Bob Foster

Perhatikan hasil pengukuran berikut.

Sumber : Buku Terpadu Fisika SMA Kelas X karya Bob Foster

Skala tetap menunjukkan : 2,5 mm
Skala putar menunjukkan : 7 x 0,01 mm = 0,07 mm
Sehingga hasil pengukurannya adalah 2,57 mm
Angka Penting
Untuk materi ini, secara detailnya bisa melihat di postingan tentang angka penting, dari pengertian, aturan penulisan sampai operasi penghitungannya.
Secara ringkasnya, aturan untuk penjumlahan/pengurangan dan perkalian/pembagian adalah sebagai berikut :
- Pada saat melakukan penjumlahan atau pengurangan, banyaknya angka penting yang dihitung didasarkan pada banyaknya angka di belakang koma yang paling sedikit.
Contohnya :
210, 5  (satu di belakang koma) + 10, 43 (dua di belakang koma) = 220,93 = 220,9 (satu angka di belakang koma)
- Pada saat melakukan perkalian atau pembagian, banyaknya angka penting yang dihasilkan sama dengan banyaknya akngak penting dari bilangan yang memiliki angka penting paling sedikit.
Contohnya :
2,21 (tiga angka penting) x 2,1 (dua angka penting) = 4,641 = 4,6 (dua angka penting)

Read More

Menghitung Resultan Vektor

Menghitung Resultan Vektor

Melanjutkan postingan kemarin yang tentang Resultan vektor yang belum ada contoh soalnya. Pada postingan kali ini, kita akan membahas resultan vektor, untuk 2 vektor yang tidak saling tegak lurus, maupun 3 atau lebih vektor.
1. Dua buah vektor, masing-masing 10 dan 8 satuan yang membentuk sudut 60⁰ satu sama lain. Tentukan resultan vektor-vektor ini?
Penyelesaian :
Sebelumnya, kita gambarkan dulu diagram vektornya untuk memperjelas permasalahan ini.

2. Perhatikan gambar berikut. Empat buah vektor gaya yang bekerja pada sebuah benda. Tentukan resultannya?
 
Penyelesaian.
Uraikan dulu vektor-vektor dalam Fx dan Fy, dengan : Fx = F cos α dan Fy = F sin α, seperti tabel berikut :

F	Sudut	Fx	Fy
10 N	300	5,00	8,66
12 N	1350	8,49	-8,49
8 N	1800	0,00	-8,00
12 N	2400	-10,39	-6,00
Jumlah		ΣFx =3,09	ΣFy =-13,83

Resultan dari vektor-vektor ini adalah :

R = 14, 17 Newton
(Catatan : penghitungan soal ini menggunakan bantuan Excel)

Read More

Penerapan Hukum Newton (1) : Soal Keseimbangan

Penerapan Hukum Newton (1) : Soal Keseimbangan

Mengutip dari buku Terpadu Fisika SMA untuk kelas X dari Bob Foster, dalam menyelesaikan soal keseimbangan yang terkait dengan hukum II Newton, ada tahap-tahap yang perlu dilakukan :
1. Gambarlah/buatlah diagram dari sistem yang akan diselesaikan
2. Gambarkan semua gaya yang bekerja pada masing-masing benda
3. Tentukan sumbu x dan sumbu y untuk mempermudah perhitungan
4. Gambarkan diagram gaya untuk masing-masing bendanya secara terpisah
5. Berdasar diagram gaya yang dibuat, tuliskan hukum II Newton dalam komponen-komponennya :
∑F_x = ma_x; ∑F_y = ma_y
Kemudian, selesaikan persamaan tersebut untuk mencari besaran yang ditanyakan.
Contoh :
Sebuah pigura digantung di dinding menggunakan tali, seperti pada gambar berikut. Jika berat pigura 10N, tentukan besar tegangan masing-masing tali?

Penyelesaian :
Gambar pada soal diperbesar untuk memperjelas dalam penguraian gaya-gaya yang bekerja.

Coba perhatikan. Dalam keadaan seimbang, berlaku :
∑F = T₁ + T₂ + W = 0
Berdasar gambar di atas, didapatkan :
∑F_X = T₂ cos 60⁰ – T₁ cos 30⁰ = 0 ……...(i)
∑F_y = T₁ sin 30⁰ + T₂ sin 60⁰ - W= 0 ……(ii)
Dari persamaan (i) didapatkan, bahwa
T₂ cos 60⁰ = T₁ cos 30⁰

Diperoleh
…………………(iii)
Dengan memasukkan ke dalam persamaan (ii) didapatkan, bahwa :
T₁ sin 30⁰ + T₂ sin 60⁰ - W= 0

2T₁ = 10, maka diperoleh :
T₁ = 10/2 = 5 N
Masukkan T₁ = 5 N ke persamaan (iii), sehingga diperoleh

Read More